11250. Рекурсия – 3

Заданы числа a, b, c. Реализуйте рекурсивную функцию:

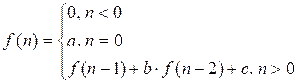
Вход. Четыре неотрицательных целых числа a, b, c (a, b, c ≤ 1000), n (0 ≤ n ≤ 1000).

Выход. Выведите значение f(n) по модулю 10⁹ + 7.

Пример входа	Пример выхода
4 2 3 3	35

РЕШЕНИЕ

рекурсия

Анализ алгоритма

В задаче следует реализовать заданную рекурсивную функцию. Используем технику мемоизации.

Реализация алгоритма

Объявим модуль MOD, по которому будут производиться вычисления. Объявим массив dp для запоминания значений функции: dp[n] = f(n).

#define MOD 1000000007

long long dp[1001];

Реализуем функцию f, указанную в условии задачи. Используем мемоизацию.

long long f(long long n)

{

if (n < 0) return 0;

if (n == 0) return a;

if (dp[n] != -1) return dp[n];

return dp[n] = (f(n - 1) + b * f(n - 2) + c) % MOD;

}

Основная часть программы. Читаем входные данные.

scanf("%lld %lld %lld %lld", &a, &b, &c, &n);

Инициализируем массив dp. Вызываем значение функции.

memset(dp, -1, sizeof(dp));

res = f(n);

Выводим ответ.

printf("%lld\n", res);

Python реализация

Увеличим размер стека для рекурсии.

import sys

sys.setrecursionlimit(10000)

Объявим модуль MOD, по которому будут производиться вычисления.

MOD = 1000000007

Реализуем функцию f, указанную в условии задачи. Используем мемоизацию.

def f(n):

if n < 0: return 0

if n == 0: return a

if dp[n] != -1: return dp[n]

dp[n] = (f(n - 1) + b * f(n - 2) + c) % MOD

return dp[n]

Основная часть программы. Читаем входные данные.

a, b, c, n = map(int, input().split())

Инициализируем список dp. В нем будем запоминать значения функции: dp[n] = f(n).

dp = [-1] * 1001

Вызываем значение функции.

res = f(n)

Выводим ответ.

print(res)